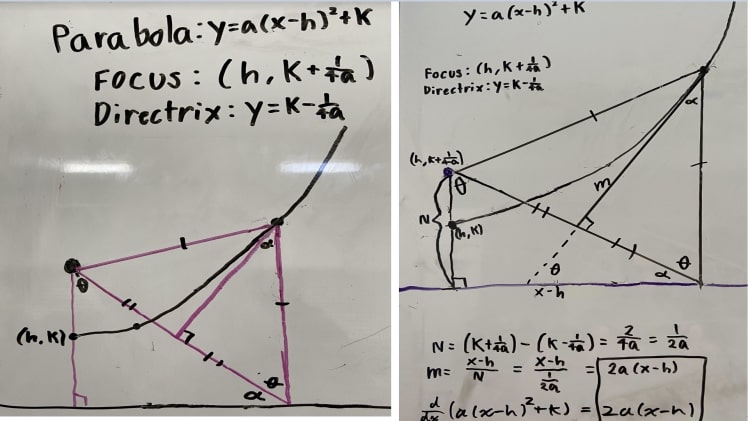
Ever spot the U-shaped parabola? Well, it is a plane curve that is defined like the mirror-symmetrical shape. In the mathematical descriptions, the parabola fits there superficially. Also, the shape is so fit in a way that the curves can be well-defined. Do you know what is the focus and directrix of parabola? Focus is a point, while directrix is simply a line on the figure.
This figure is interesting! Wherever you draw a line on the directrix, it will always be at an equal distance from the center.
How Would You Perfectly Define Parabola?
A parabola can be defined as the section of the right circular cone which runs parallelly towards the generator of the cone. The Parabola is a section of the right circular cone which is located on a plane structure and is at a distance which is from a fixed point known as the focus to an equal distance to another fixed line which is defined as the directrix.
So, what did we learn from here?
Summing up,
- The fixed point is known as the focus of the Parabola
- The fixed-line on the Parabola is called the directrix.
What is the Equation of Parabola?
- y2 = x is the equation of parabola. This equation is valid only when the directrix runs parallelly towards the y-axis.
- x2 = 4ay is the standard equation of the parabola, if it runs sideways which is sideways to the directrix that is parallel to the x-axis.
So, what happens when the parabola is in negative quadrants? This time the formula of the equation of parabola will be y2 = 4ax and x2 = 4ay
Do You Know the Equation of Hyperbola?
Before studying the equation of the hyperbola, first, let us discuss what is hyperbola?
The Hyperbola is being discussed in analytical geometry. This structure forms the conic section which is formed by intersecting a circular cone that is rightly aligned and is located on a plane-like structure that has both the halves in the intersected plane.
Have you studied the ellipse? Just like the ellipse, a hyperbola is defined as a set of points that lie in a coordinate region.
What is a Hyperbola Equation?
x2a2−y2b2=1 – this is the equation that represents the general equation of the hyperbola structure. But what do x and y represent? So, X-axis is the transverse axis of the hyperbola while the Y-axis is known as the conjugate axis of the hyperbola.
How Would You Define the Standard Equation of Hyperbola?
Here we will actually talk about two equations of Hyperbola. They are:
- x2a2−y2b2=1x2a2−y2b2=1
- y2a2−x2b2=1y2a2−x2b2=1
The first equation is the standard equation of hyperbola which is primarily based on the transverse axis and the other in the conjugate axis of each of the hyperbolic structures.
While the second equation is also a standard equation of the hyperbola which has the transverse axis as the Y-axis and the conjugate axis as the X-axis.
Formula of Hyperbola
As previously studied, Hyperbola is the open curve that has two branches that look like mirror images of the other one.
Right for any point on the branch, this is the absolute difference between the point and from the foci which is constant and equal to 2a, this ‘a’ is the distance of the branch from the central point. This hyperbola formula assists us in estimating the different types of parameters related to this figure. With this help, we can find out the equation of Hyperbola, the major and the minor axis can be calculated.
This study was primarily focused on Parabola and Hyperbola. We present other fresh topics as well. Visit Cuemath and learn your favorite mathematical concepts. We provide a range of fun and interesting topics which are easy and ready to be grasped by anyone.